Probabilités : les bases, les arbres pondérés, expériences aléatoires à deux épreuves

Langage et savoir de base

• Une expérience aléatoire est une expérience dont on connaît à l'avance l'ensemble des résultats (ou issues) possibles.
  • Le lancer de dés, la loterie, le tirage de jetons ou de boules contenus dans une urne sont des expériences aléatoires.
• L'univers est l'ensemble de tous les résultats (ou issues) possibles. Ainsi, lorsque l'on lance un dé de jeu, l'ensemble des issues possibles sont : 1, 2, 3, 4, 5, 6.
• Un événement élémentaire ne comporte qu'une possibilité. Ainsi, "obtenir le chiffre 2" en lançant un dé correspond à un événement élémentaire. "Obtenir le chiffre 3" correspond à un autre événement élémentaire.
• Un événement est une partie de l'univers, il est constitué par une ou plusieurs issues de l'expérience. Ainsi, lors d'un lancement de dé, "obtenir un chiffre impair" correspond aux issues : 1, 3, 5.
• Une probabilité est un nombre compris entre 0 et 1. 0 équivaut à un événement impossible et 1 à un événement certain.
• La somme des probabilités de toutes les issues d'une expérience aléatoire est égale à 1.
  • Ainsi, la somme de toutes les issues d'un lancement de dé :



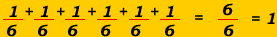
• Lorsque toutes les issues d'une expérience aléatoire ont la même probabilité, on dit que les issues sont équiprobables. Dans ce cas, on peut calculer la probabilité d'un événement grâce à la formule suivante :

• Exemple : lors du lancement d'une pièce de monnaie non truquée, il y a autant de chances d'obtenir pile que face. Considérons l'événement X "obtenir pile", p(X) = 1/2. (Il y a une issue correspondant à l'événement (pile) et il y a deux issues possible au total (pile et face).

Exemple élémentaire : On a une urne (boîte) contenant 4 boules numérotées de 1 à 4 dans laquelle on tire une boule au hasard..

• Quels sont les événements élémentaires que l'on peut rencontrer ?
  • Les événements élémentaires sont : "obtenir 1", "obtenir 2 ", "obtenir 3 ", "obtenir 4 ". Nota : dans cette question, il s'agit de décrire toutes les issues possibles).
• Quelle est la probabilité d'obtenir la boule numéro 2 ?
  • Le nombre total d'issues possibles est 4. La probabilité d'obtenir la boule 2 est donc de 1/4 (1 chance sur 4 possibilités en tout d'obtenir la boule 2). Donc p("obtenir 2") = 1/4.
• Quelle est la probabilité d'obtenir un chiffre pair ?
  • Il y a 1 chance sur 4 d'obtenir un 2 : p(obtenir 2) = 1/4 et il y a 1 chance sur 4 d'obtenir un 4 : p(obtenir 4) = 1/4. => cela correspond aux issues 2 et 4.
    • obtenir un résultat pair est un événement réalisé par deux issues : 2 et 4
  • Par conséquent, p("obtenir un chiffre pair") = 1/4 + 1/4 = 2/4 = 1/2 (on ajoute les probabilités des événements élémentaires : "obtenir 2" et "obtenir 4". Nota : en général on présente une probabilité sous la forme d'une fraction irréductible.

Arbre pondéré ou arbre des possibles

• Pour calculer la probabilité d'un événement, on additionne les possibilités figurant sur les branches de l'arbre pondéré.

• Exemple 1 : On lance un dé cubique.
  • Quel est le nombre d'issues possibles ?
    • il y a 6 faces différentes, donc 6 issues possibles.
  • Quels sont les événements possibles ?
    • Il y a 6 événements possibles : "obtenir un", "obtenir 2", "obtenir 3 ", "obtenir 4 ", "obtenir 5 ", "obtenir 6 ".
• Quelle est la probabilité d'obtenir un chiffre impair ?
  • p(obtenir un chiffre impair) = p(obtenir 1) + p(obtenir 3) + p(obtenir 5) = 1/6 + 1/6 + 1/6 = 3/6 = 1/2.



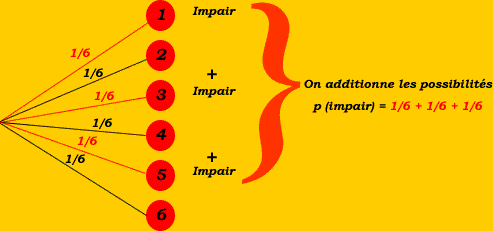
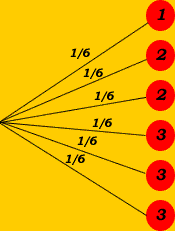
• Exemple 2 : une urne contient 6 boules numérotées ainsi : trois boules numéro 3, deux boules numéros 2 et une boule numéro 1.

Evénements particuliers

En probabilité, il existe des événements particuliers :

• Un événement est dit impossible si sa probabilité vaut 0 (c'est-à-dire qu'il ne se produira jamais).
  • Dans le lancement d'un dé cubique, l’événement A : "obtenir 7" est impossible et p(A) = 0
• Un événement est dit certain si sa probabilité vaut 1 (c'est-à-dire qu'il se produira obligatoirement).
  • exemple : la probabilité qu'un homme meurt un jour est dit certain et vaut 1 (un jour et de manière certaine, cet événement se produira).
  • Dans le lancement d'un dé cubique , l’événement A : "obtenir un nombre inférieur ou égal à 6 " est certain et p(A) = 1.
• Deux événements sont incompatibles s'ils ne peuvent pas se produire en même temps.
  • Lorsque l'on lance une pièce en l'air les événements "avoir pile" et "avoir face" sont incompatibles.
• Un événement et son contraire sont incompatibles. Donc, la somme de leurs probabilités vaut 1. Le contraire d'un événement A se note non A. p(A) + p(non A) = 1. On peut également l'écrire : .
  • Exemple : lors d'un lancé de dé cubique, on calcule l'événement contraire à A ("obtenir 1") => c'est-à-dire ne pas obtenir 1, donc :
    • p(non A) = 1 - p(A) = 1 - 1/6 = 5/6.

Expériences aléatoires à deux épreuves

Dans une expérience à plusieurs épreuves, la probabilité d'un événement est égale au produit des probabilités rencontrées le long du chemin qui mène à cet événement.

Exemple 1 : On tire d’abord une boule dans la boîte A et on note sa couleur. Ensuite, on tire une boule dans la deuxième boîte B et on note la couleur.

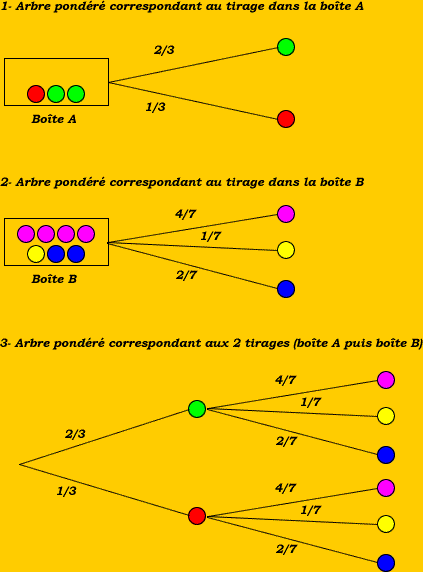
Quelle est la probabilité d'obtenir une boule rouge et une boule jaune ?

La probabilité d'obtenir le rouge et le jaune = au produit des probabilités rencontrées le long du chemin qui mène à cet événement. p(rouge, jaune) = 1/3 x 1/7 = 1/21

Exemple 2 : on lance l'une après l'autre deux pièces de monnaie.

L'arbre ci-dessous décrit les situations possibles.

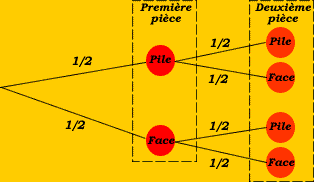
Quelle est la probabilité d'obtenir le côté pile pour chacune des pièces ?

La probabilité d'obtenir pile pour les deux pièces = au produit des probabilités rencontrées le long du chemin qui mène à cet événement. p(pile, pile) = 1/2 x 1/2 = 1/4.

Exemple 3 : on fait tourner les deux roues du jeu arc-en-ciel. On fait trourner la roue bicolore en premier puis la tricolore.

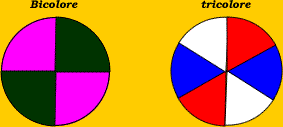
L'arbre pondéré ci-dessous décrit les situations possibles :

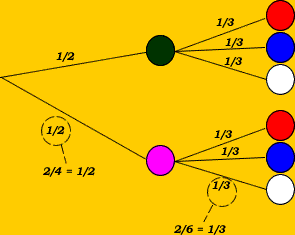
Quelle est la probabilité d'obtenir le vert et le rouge ?

La probabilité d'obtenir le vert et le rouge = au produit des probabilités rencontrées le long du chemin qui mène à cet événement. p(vert, rouge) = 1/2 x 1/3 = 1/6