Cours de maths et exercices : les puissances de n et de 10 (calcul, propriétés, opérations, écriture scientifique)
Cours et exercices de maths - les puissances : nombres relatifs et puissances de n et de 10

Mathématiques

Les puissances de n et de 10

imprimer la fiche

imprimer la fiche

 Exercices d'anglais
Les cours de maths concours, au collège ( 6ème, 5ème, 4èmeet 3ème) et au primaire (cm2, cm1, ce2, ce1, cp)

MathématiquesDéfinition générale

Dans la puissance an, le a désigne la base et n l'exposant.

puissance d'un nombre relatif

 

Exemples :

  • 2 x 2 x 2 = 23 (se lit : 2 à la puissance 3)
  • 4 x 4 x 4 = 43 (se lit : 4 à la puissance 3)
  • 4 x 4 = 42 (se lit : 4 à la puissance 2)
  • 4 = 41 (se lit : 4 à la puissance 1)
  
  • 5 x 5 x 5 = 53 (se lit : 5 exposant 3)
  • 6 x 6 x 6 x 6 = 64 (se lit : 6 exposant 4)
  • a x a = a2 (se lit : a exposant 2)
  • a x a x a x a = a4 (se lit : a exposant 4)

 

MathématiquesCalcul d'une puissance

Voici quelques exemples pour bien comprendre...

  • 23 = 2 x 2 x 2 = 8 => base = 2, exposant=3
  • -23 = -2 x 2 x 2 = -8 => base = 2, exposant=3
  • -22 = -2 x 2 = -4 =>base = 2, exposant=2
  • (-2)2= (-2) x (-2) = 4 => base = -2, exposant=2
  • (-2)3= (-2) x (-2) x (-2) = -8 => base = -2, exposant=3
  
  • 53 = 5 x 5 x 5 = 125
  • -53 = -5 x 5 x 5 = -125
  • -52 = -5 x 5 = -25
  • (-5)2= (-5) x (-5) = 25
  • (-5)3= (-5) x (-5) x (-5) = -125

 

MathématiquesDéfinition de a0, a-1 et a-n

Puissance négative

 

MathématiquesOpérations sur les puissances

Manipulez beaucoup et apprenez par coeur les différentes propriétés...

Opérations sur les puissances des nombres relatifs

 

MathématiquesLes puissances de 10

Pour les puissances de 10 on applique les mêmes règles que pour les puissances des nombres relatifs... Reprenons les exemples vus auparavent avec des puissances de 10.

 

Opérations sur les puissances de 10.

 

A savoir...

à savoir sur les puissances de 10 : exposant positif et négatif

 

 

 

MathématiquesLe saviez-vous ?

  1. Pour calculer une suite d'opérations, il faut respecter un certain ordre...
    1. calculer l'intérieur des parenthèses,
    2. calculer les puissances,
    3. calculer les multiplications et les divisions,
    4. calculer les additions et les soustractions.

Exemples :

  • (3 x 5)² = (15)² = 225
  • (3²x2)² = (9x2)² = (18)² = 324
  • 10² x 3 + 4 = 100 x 3 + 4 = 300 + 4 = 304
  • 5 + 3² = 5 + 9 = 14
  • 6² - (9-3)² + 3x3 - 27:9 = 6² - (6)² + 3x3 - 27:9 = 6² - 6² + 9 - 9 = 0
  1. Lorsque l'on multiplie par une puissance de 10 cela revient à déplacer la virgule à droite (si l'exposant est positif) ou à gauche (si l'exposant est négatif).

 

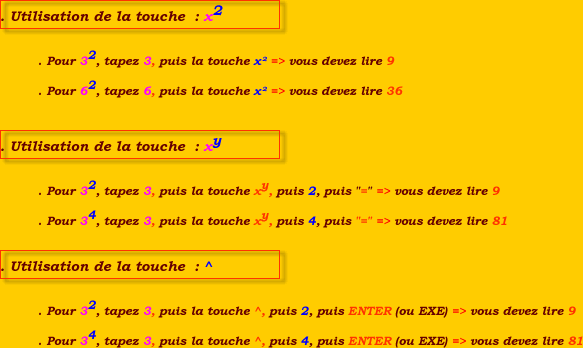
puissance de 10 et décalage à droite et à gauche

 

 

MathématiquesCalculer les puissances avec une calculatrice

Selon la calculatrice que vous utilisez, vous pourrez procéder de différentes manières :

 

utiliser la calculatrice pour calculer des puissances